Différence entre Sin 2x et 2 Sin x

Sin 2x vs 2 Sin x

Les fonctions sont l'une des classes les plus importantes d'objets mathématiques, largement utilisés dans presque tous les sous-domaines mathématiques. La fonction sinusoïdale dénotée f (x) = sin x est une fonction trigonométrique définie à partir de l'ensemble des nombres réels sur l'intervalle [-1, 1] et est périodique avec la période 2ᴫ.

La définition de base du sinus d'un angle aigu se fait en utilisant un triangle rectangle. Le sinus de l'angle est égal au rapport de la longueur du côté opposé à un angle à la longueur de l'hypoténuse. Cette définition peut être étendue à tous les angles en utilisant les identités sin (- x) = - sin x et sin (ᴫ + x x et sin (2 n ᴫ + x) = sin x.

= x et g (< x) = 2 x. Qu'est-ce que Sin 2x? Considérons la fonction composite brouillard donnée par

brouillard

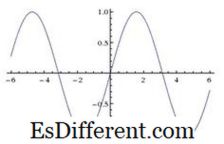
(x) = x)) = f (2 x) = sin 2 x. Cette fonction est assez similaire à sin x avec le domaine comme l'ensemble des nombres réels et la gamme comme intervalle [-1, 1]. Cette fonction est périodique avec la période ᴫ (par opposition à la période 2ᴫ de sin x). Sin 2 x peut être étendu par l'identité Sin 2 x = 2 sin x cos x.

Qu'est-ce que 2 Sin x? Considérons la fonction composite gof donnée par

gof

(

x) = g x)) = g (sin x) = 2 sin x. C'est aussi une fonction périodique avec la même période que sin x, mais deux fois l'amplitude de celle-ci puisque -1 ≤ sin x ≤ 1 implique -2 ≤ 2 sin x ≤ 2. Son domaine est l'ensemble des nombres réels et la gamme est l'intervalle [-2, 2] Quelle est la différence entre Sin 2x et 2 Sin x? • Sin 2x est défini à partir de l'ensemble des nombres réels sur l'intervalle [-1, 1], alors que 2Sin x est défini à partir de l'ensemble des nombres réels sur l'intervalle [-2, 2]. • Sin 2x est périodique avec la période ᴫ mais 2 Sin x est périodique avec la période 2ᴫ.